Mr. P and the Multiverse of Madness

library(rethinking)
library(tidyverse)
library(riekelib)

Between my job as a consumer experience analyst and my side-interest in electoral forecasting, I spend a lot of time digging into survey data. Surveys are great! But the survey sample may not always be representative of the population. When this is the case, we can’t take the aggregated survey responses at face value and need to adjust for any bias the non-representativeness may have introduced.

Multilevel regression and post-stratification (which gets re-dubbed as MRP or “Mr P”) is a super intimidating and stats-y sounding procedure to correct for this bias, but it turns out it’s actually not too difficult. MRP is a two step process that involves fitting a multilvel model based (at least in part) on the demographic variables tied to each response, then reweighting so that the sample demographics match the population demographics. Let’s run through an example!

The Setup

Let’s suppose that Harris County, TX, is proposing a new law and want to know if residents support it or not. As a part of the survey, they plan to collect data on race. According to 2020 census data, white and hispanic residents make up a majority of the county.

# harris county demographic data (2020, wikipedia)
demographics <- 
  tribble(
    ~race, ~pop,
    "white", 1309593,
    "black", 885517,
    "native american", 8432,
    "asian", 344762,
    "pacific islander", 3199,
    "other", 23262,
    "mixed", 121671,
    "hispanic", 2034709
  )

demographics %>%
  arrange(desc(pop)) %>%
  mutate(race = str_to_title(race),
         pop = scales::label_comma()(pop)) %>%
  rename_with(str_to_title) %>%
  knitr::kable()

Race	Pop
Hispanic	2,034,709
White	1,309,593
Black	885,517
Asian	344,762
Mixed	121,671
Other	23,262
Native American	8,432
Pacific Islander	3,199

The county plans on sending out the survey randomly. If, however, the different racial groups respond at different rates, they may be over or under-represented in the survey responses. Here, I’ve set a fake response rate and approval rate for each racial group — despite making up over 40% of the actual population in Harris county, hispanics will be under-represented in the survey relative to white residents because they respond at a lower rate. White respondents are far less likely to approve of the new law, so the results of the survey will be biased downwards.

# assign demographic weights & parameters
demographics <- 
  demographics %>%
  mutate(pop_rate = pop/sum(pop)) %>%
  bind_cols(response_rate = seq(from = 0.4, to = 0.2, length.out = nrow(.))) %>%
  mutate(survey_weight = pop_rate * response_rate,
         survey_weight = survey_weight/sum(survey_weight)) %>%
  bind_cols(approval_rate = seq(from = 0.2, to = 0.9, length.out = nrow(.)))

demographics %>%
  arrange(desc(pop)) %>%
  mutate(race = str_to_title(race),
         pop = scales::label_comma()(pop),
         across(c(pop_rate:approval_rate), ~scales::label_percent(accuracy = 0.1)(.x))) %>%
  rename_with(~str_replace(.x, "_", " ")) %>%
  rename_with(str_to_title) %>%
  knitr::kable()

Race	Pop	Pop Rate	Response Rate	Survey Weight	Approval Rate
Hispanic	2,034,709	43.0%	20.0%	29.0%	90.0%
White	1,309,593	27.7%	40.0%	37.3%	20.0%
Black	885,517	18.7%	37.1%	23.4%	30.0%
Asian	344,762	7.3%	31.4%	7.7%	50.0%
Mixed	121,671	2.6%	22.9%	2.0%	80.0%
Other	23,262	0.5%	25.7%	0.4%	70.0%
Native American	8,432	0.2%	34.3%	0.2%	40.0%
Pacific Islander	3,199	0.1%	28.6%	0.1%	60.0%

Simulating 1300 responses results in an aggregated result just shy of 50%. If you take this result as-is, it means that the majority of Harris county residents do not support the new law.

set.seed(1999)
races <- 
  sample(
    demographics$race,
    size = 1300,
    replace = TRUE,
    prob = demographics$survey_weight
  )

set.seed(1998)
surveys <- 
  tibble(race = races) %>%
  left_join(demographics %>% select(race, approval_rate)) %>%
  bind_cols(approve = rbinom(nrow(.), 1, .$approval_rate)) %>%
  select(-approval_rate)

surveys %>%
  percent(approve, .keep_n = TRUE) %>%
  mutate(n = sum(n)) %>%
  filter(approve == 1) %>%
  select(-approve) %>%
  mutate(n = scales::label_comma()(n),
         pct = scales::label_percent(accuracy = 0.1)(pct)) %>%
  rename(Responses = n,
         `Approval %` = pct) %>%
  knitr::kable()

Responses	Approval %
1,300	49.5%

If we break out by race, however, we can see that there is a lot of variation among the different demographic groups — and some didn’t get surveyed at all!

surveys %>%
  group_by(race) %>%
  percent(approve, .keep_n = TRUE) %>%
  mutate(n = sum(n)) %>%
  bind_rows(tibble(race = "native american", approve = 1, n = 1, pct = 0)) %>%
  filter(approve == 1) %>%
  right_join(demographics) %>%
  select(race, n, pct) %>%
  mutate(n = replace_na(n, 0)) %>%
  arrange(desc(n)) %>%
  mutate(race = str_to_title(race),
         pct = scales::label_percent(accuracy = 0.1)(pct)) %>%
  rename(Race = race,
         Responses = n,
         `Approval %` = pct) %>%
  knitr::kable()

Race	Responses	Approval %
White	445	20.4%
Hispanic	401	91.8%
Black	309	30.7%
Asian	111	55.9%
Mixed	33	81.8%
Native American	1	0.0%
Pacific Islander	0	NA
Other	0	NA

This survey is clearly not representative of the overall population! However, we don’t necessarily need to spend a bunch of time, energy, and resources conducting another survey. Instead, we can use MRP to estimate the overall county support from the non-representative survey data.

The Execution

Multilevel regression

The first stage of MRP is to fit a model to the data. Modeling isn’t actually needed for post-stratification, but is useful for estimating average effects. Multilevel models let us pool information across groups (i.e., groups with few responses will get shrunken towards the group mean), and doing so with a Bayesian flavor gives us the added benefit of propogating our prior uncertainty through the model.

In this case, we’re interested in the level of support in the population, \(\pi\). We can estimate \(\pi\) by modeling each individual’s probability of approving, \(\pi_i\), based on an average level of support, \(\alpha\), offset by some amount based on the respondent’s race, \(z_{\text{race}[i]} \ \sigma\).

\[ \begin{align*} \text{Approval}_i & \sim \text{Bernoulli}(\pi_i) \\ \text{logit}(\pi_i) & = \alpha + z_{\text{race}[i]} \ \sigma \\ \alpha & \sim \text{Normal}(0, 1) \\ z_{\text{race}} & \sim \text{Normal}(0, 0.5) \\ \sigma & \sim \text{Exponential}(1) \end{align*} \]

rids <- 
  surveys %>%
  distinct(race) %>%
  arrange(race) %>%
  bind_cols(rid = seq(1:nrow(.)))

surveys_stan <- 
  surveys %>%
  left_join(rids) %>%
  select(approve, rid) %>%
  as.list()

set.seed(1997)
support_mod <-
  ulam(
    alist(
      approve ~ dbinom(1, p),
      logit(p) <- alpha + z[rid]*sigma,
      alpha ~ dnorm(0, 1),
      z[rid] ~ dnorm(0, 0.5),
      sigma ~ dexp(1)
    ),
    
    data = surveys_stan,
    chains = 4,
    cores = 4,
    iter = 1000
  )

If we plug into a model, we can estimate the level of support among each racial group. Because this is a multilevel model, we can estimate the level of support among groups for which there are no survey responses using the global average, \(\alpha\) and the prior estimate for \(z\). This doesn’t tell us a whole lot in this case other than the prior is very uncertain (but this makes sense given how spread out each racial subset is).

# get posterior draws as a tibble
draws <- 
  support_mod@stanfit %>%
  posterior::as_draws_df() %>%
  as_tibble()

races <- 
  demographics %>%
  left_join(rids) %>%
  select(race, rid)

# pacific islander/other had no responses, so only can use the 
# alpha term from the model for these groups
# z is estimated from the prior
set.seed(1996)
unknown_draws <- 
  draws %>%
  select(.draw, alpha, sigma) %>%
  bind_cols(z = rnorm(nrow(.), 0, 0.5))
  
unknown_draws <- 
  bind_rows(unknown_draws %>% mutate(race = "pacific islander"),
            unknown_draws %>% mutate(race = "other")) 

# convert to long format for working with plots
draws <- 
  draws %>% 
  select(starts_with("z"), .draw) %>%
  pivot_longer(starts_with("z"),
               names_to = "rid",
               values_to = "z") %>%
  mutate(rid = as.integer(str_extract(rid, "[:digit:]"))) %>%
  left_join(draws) %>%
  select(-starts_with("z[")) %>%
  left_join(rids) %>%
  select(.draw, race, z, alpha, sigma) %>%
  bind_rows(unknown_draws)

draws %>%
  mutate(approve = expit(alpha + z*sigma),
         race = fct_reorder(str_to_title(race), approve)) %>%
  ggplot(aes(x = race,
             y = approve)) +
  ggdist::stat_slabinterval(alpha = 0.65,
                            fill = RColorBrewer::brewer.pal(3, "Dark2")[3],
                            breaks = seq(from = 0, to = 1, by = 0.00625),
                            slab_color = "white",
                            slab_size = 1,
                            slab_alpha = 0.5,
                            .width = c(0.5, 0.8),
                            outline_bars = TRUE) +
  scale_y_continuous(labels = scales::label_percent()) + 
  coord_flip() +
  theme_rieke() +
  labs(title = "Racing to Support",
       subtitle = "Estimated level of support for the new law by racial group",
       x = NULL,
       y = NULL,
       caption = "Pointrange indicates 50/80%<br>posterior credible interval")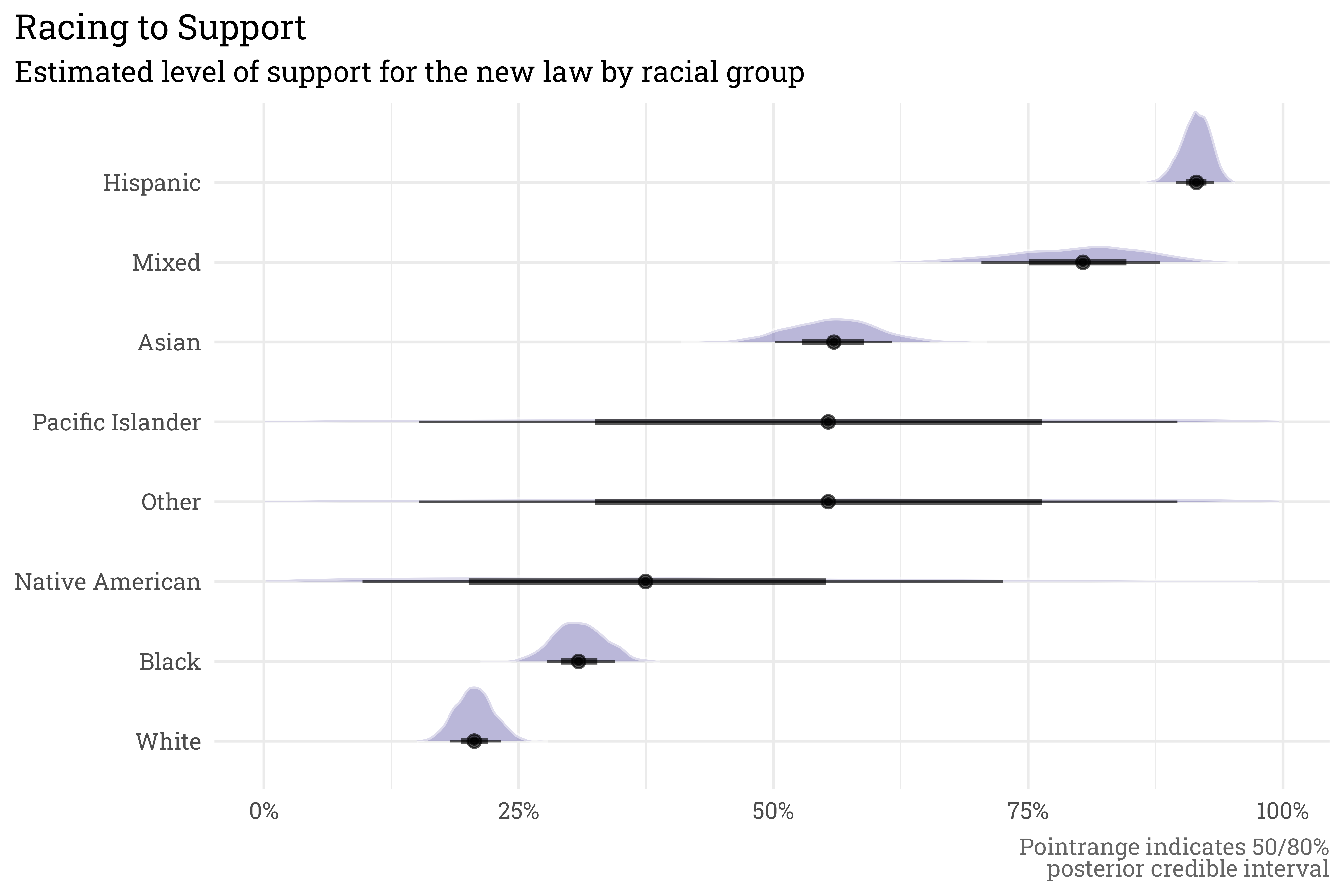

Post-stratification

The survey’s raw estimate for \(\pi\) (even after modeling) is biased, since our survey population is not a good proxy for the county’s population. What we want is to adjust \(\pi\) based on the relative weight of each racial group in the county. We can get this by summing up for all races \(\text{n}\) the level of support for that race, \(\pi_{\text{race}[i]}\), multiplied by the proportion in the population, \(p_{\text{race}[i]} \ / \ p_{\text{total}}\).

\[ \begin{align*} \pi_{\text{population}} & = \sum_{i = 1}^{\text{n}} \frac{\pi_{\text{race}[i]} \times p_{\text{race[i]}}}{p_{\text{total}}} \end{align*} \]

Doing so with a Bayesian model means that the uncertainty in the survey data is represented in the post-stratified data. In this case, the support among the survey respondents suggested that the county was just about dead-even in approval/disapproval of the new law. The post-stratified results, however, tell a different story: even with uncertainty, a majority of residents clearly approve.

survey_pcts <- 
  surveys %>%
  percent(race)

respondent_approval <- 
  draws %>%
  left_join(survey_pcts) %>%
  mutate(pct = replace_na(pct, 0),
         approve = expit(alpha + z*sigma)) %>%
  group_by(.draw) %>%
  summarise(approve = sum(pct * approve)) 
  
population_approval <- 
  draws %>%
  left_join(demographics) %>%
  select(.draw:pop_rate, -pop) %>%
  mutate(approve = expit(alpha + z*sigma)) %>%
  group_by(.draw) %>%
  summarise(approve = sum(pop_rate * approve)) 

population_approval %>%
  rename(population = approve) %>%
  left_join(respondent_approval) %>%
  rename(respondents = approve) %>%
  pivot_longer(c(population, respondents),
               names_to = "group",
               values_to = "approve") %>%
  ggplot(aes(x = approve,
             fill = group)) + 
  geom_histogram(position = "identity",
                 alpha = 0.75,
                 bins = 40,
                 color = "white") +
  scale_fill_brewer(palette = "Dark2") +
  scale_x_continuous(labels = scales::label_percent()) + 
  theme_rieke() +
  labs(title = "Realigning Reality: Post-stratification tells a different story",
       subtitle = glue::glue("Estimated support among **",
                             "{color_text('survey respondents', RColorBrewer::brewer.pal(3, 'Dark2')[2])}",
                             "** and **",
                             "{color_text('the general population', RColorBrewer::brewer.pal(3, 'Dark2')[1])}",
                             "**"),
       x = NULL,
       y = NULL,
       caption = "Post-stratification weights based on 2020<br>Harris County demographic data") +
  theme(legend.position = "none",
        axis.text.y = element_blank())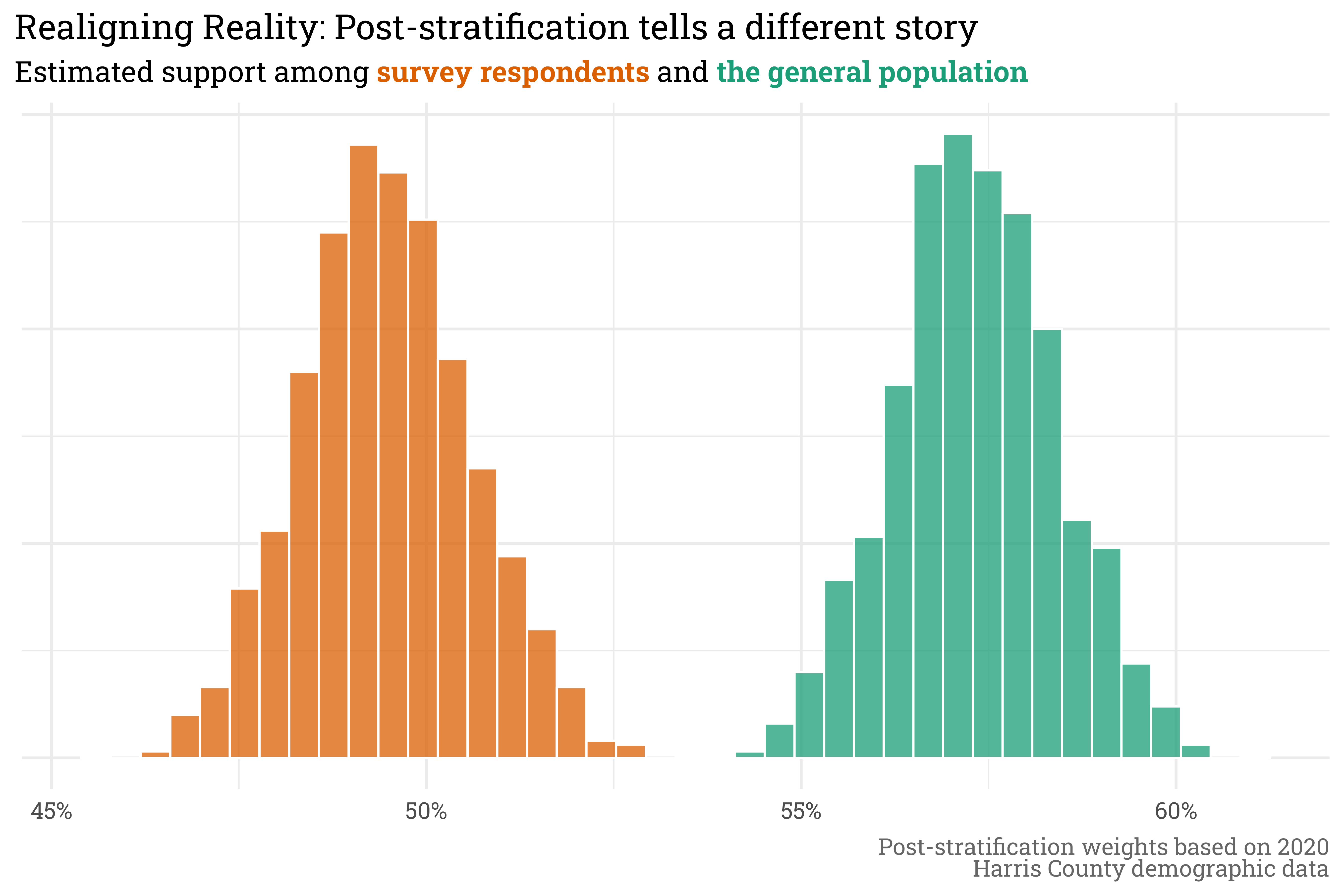

Some closing thoughts

MRP here was only used with one indicator variable for race but could be extended extended to any number of variables, provided you know the cross-sectional data for each combination within the sample and the population (for example, if I wanted to post-stratify on gender and age, I’d need to know the total number of young men, young women, old men, and old women). I’ve used this in the context of demographic variables, but this could also be extended to any indicator variable. For example, I could use MRP to estimate patient satisfaction based on race, gender, and hospital procedure code if need be.